查找

1.学习总结(2分)

1.1查找的思维导图

各种查找的时间复杂度，ASL成功，不成功。都要体现。

1.2 查找学习体会

谈谈你对查找算法学习体会。也可以谈谈STL容器中查找如何用的。
1.数据结构与算法的内容还有很多。但是由于时间的关系，我并没有深入下去，尤其是查找时用到的平衡二叉树、B_和B+树，还有红黑树等等。希望以后有时间可以继续看。
2.Map是STL的一个关联容器，它提供一对一（其中第一个可以称为关键字，每个关键字只能在map中出现一次，第二个可能称为该关键字的值）的数据 处理能力，由于这个特性，它完成有可能在我们处理一对一数据的时候，在编程上提供快速通道。这里说下map内部数据的组织，map内部自建一颗红黑树(一 种非严格意义上的平衡二叉树)，这颗树具有对数据自动排序的功能，所以在map内部所有的数据都是有序的，后边我们会见识到有序的好处

2.PTA实验作业（4分）

本周要求挑选出3道题目书写设计思路、调试过程。设计思路使用伪代码描述。题目选做要求：
不能选6-1，6-4
具体书写内容及格式如下：

2.1 题目1：是否二叉搜索树（25 分）

2.2 设计思路（伪代码或流程图）

因为一个二叉搜索树的先序遍历是呈现递增的，
利用这一特性，来判断二叉树是否为搜索二叉树。
 先定义一个静态变量 max =-1；
 if（在树不为空的情况下）{
    递归（左子树）
    判断max 和 T->data值得大小 
    if （max更小）说明目前还符合搜索树的要求，
    else 说明不符合二叉搜索树的要求。
    递归（右子树）
}

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

2.4 PTA提交列表说明。

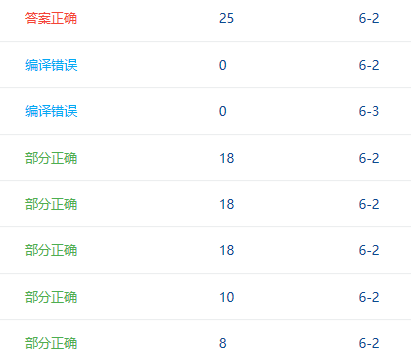
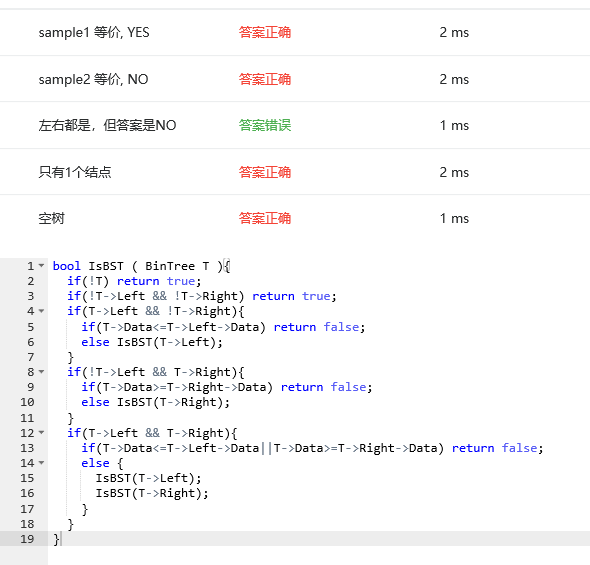
最初我利用的不是先序遍历这个方法我是遍历二叉树，让每次数的节点的值与他的左子树与右子树进行比较，
如果，左子树比该节点的值更大就符合，相反就矛盾，但是这样有一个问题就是，不能隔代比较，这样就导致错误。

2.1 题目2 二叉搜索树中的最近公共祖先

2.2 设计思路（伪代码或流程图）

定义两个结构体变量，trmp1,temp2;
if（树为空），说明查找错误，
在树不空的情况下{
  if（if(u<T->Key并且v>T->Key){
        if（T->Left->Key==u并且T->Right->Key==v）说明 T为公共祖先。
       否则{
             tmp1=tmp2=T;
          while（temp1不为空）{
                         寻找与u相等的值
}
         while（temp2不为空）{
             寻找与v相等的值}
if（都找到与u，v相等的值）说明T为他们的祖先。
	if(u<T->Key并且v<T->Key){
			LCA(T->Left,u,v);
递归左子树
		}
		if(u>T->Key&&v>T->Key) LCA(T->Right,u,v);
递归右子树
		
	}

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

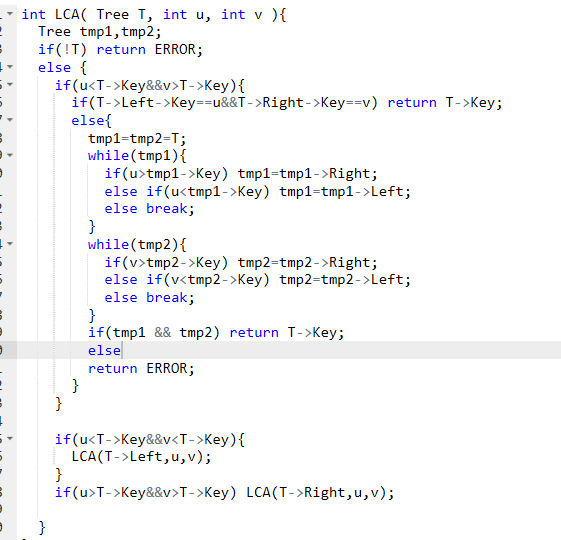
2.4 PTA提交列表说明。

这道题没什么问题

2.1 题目3 7-2 航空公司VIP客户查询（25 分）

2.2 设计思路（伪代码或流程图）

定义一个 map<string,int> vip;
将客户的 身份证号跟里程数，录入到map中，
每次录入的时候遍历map 寻找是否曾经录入过此客户，
如果相同，将其里程数相加即可。
否则 录入。
之后的查找也是遍历
if（号码匹配）输出里程数
else 输出No Info

2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）

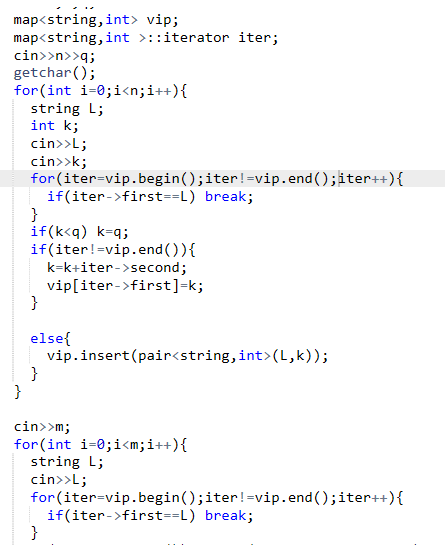
2.4 PTA提交列表说明

林丽老师说用cin cout 会导致运行超时，我也不知道为什么，就全部转化成c的就可以通过。

3.截图本周题目集的PTA最后排名（3分）

3.1 PTA排名（截图带自己名字的排名）

3.2 我的总分：130

4. 阅读代码（必做，1分）

红黑树的旋转、查找和删除
红黑树的节点声明，其中Parent指针是指向某一节点的父节点的指针：
typedef struct TreeNode *PtrRBTNode;
typedef struct TreeNode RBTNode;
struct TreeNode{
ElementType Key;
ColorType Color;
PtrRBTNode Left;
PtrRBTNode Right;
PtrRBTNode Parent;
};
红黑树的插入操作和BST也差不多，同样在插入以后需要像AVL树那样向上调整，但是红黑树因为每个节点都存在parent指针，所以向上调整可以通过迭代来实现，而不需要像AVL树那样要用递归回溯。红黑树向上调整的过程实际上就是不断将新插入的红节点向上移动，直至它的父节点为黑为止，这样就存在三种情况（之所以不存在其他情况，完全是由于红黑树的性质决定的）。并且红黑树的根节点和根节点的父节点的Color一定是Black，所以这个向上调整的过程就一定会停止，也就是最终一定能跳出循环，在跳出循环之后需要将根节点的Color赋值为Black。
以下三种情况均针对待调整节点在其祖父节点的左子树中时进行分析，若在右子树中时，做对称操作即可。
Case One
这种情况中,待调整节点是C节点，C节点的父节点B和父节点B的Sibling节点E的Color均为Red（需要注意的是这里C、D、E的左右子树可能为空，可能不为空，且A节点也可能不是根节点）。遇到这种情况时，将C节点的父节点B和父节点B的Sibling节点E的Color赋值为Black，并将C节点的祖父节点A赋值为Red，同时将待调整节点变为节点A。因为起初父节点的Color为Red，所以根据性质，C的祖父节点A的Color一定为Black，这样同时调整B和E为Black，可以使沿B和E至叶节点的路径上的Black节点数相同，且消除了B、C均为Red的情况，但是这样一来沿A至叶节点的路径上的Black节点数就增加了一个，因此将A赋值为Red，使得沿A至叶节点的路径上的Black节点数保持和调整前的数量一致，然而我们无法排除A的父节点的Color也是Red的情况，所以将待调整节点变为节点A，在下一次循环中继续调整。
Case Two
这种情况中，待调整节点是D节点，D节点的父节点B的Color是Red，但是父节点B的Sibling节点E的Color是Black，且D节点是其父节点B的右子节点。此时仅需要以B节点为Pivot做左旋即可，并将待调整节点变为B。在具体实现时还需要注意将记录父节点的变量FNode变为D节点，并进入Case Three。之所以要这样操作，是因为这里的操作仅仅针对两个Red节点，而对于Black节点的操作（例如C节点），起初沿B的左子节点、D的左（C节点）右子节点至叶节点的路径的Black节点数都是相同的，所以旋转操作中移动以C为根节点的子树后，沿B的子节点和D的子节点至叶节点的路径的Black节点数依然是相同的且保持不变。
Case Three
这种情况中，待调整节点是C节点，C节点的父节点B的Color是Red，但是父节点B的Sibling节点E的Color是Black，且C节点是其父节点B的左子节点。此时仅需要以C节点的祖父节点A作为Pivot做右旋即可，并将原先的父节点B的Color调整为Black，将原先的祖父节点A的Color调整为Red。之所以要这样操作，是因为起初沿C节点的左右子节点、沿D节点和E节点至叶节点的路径的Black节点数是相同的，所以在调整过后沿它们至叶节点的路径上的Black节点数依然是相同的且保持不变，而这样操作却可以通过交换颜色将一个Red节点移动到祖先节点的右子树中，消除了两个Red节点相连的情况，当然旋转后新的子树的根节点B要赋值为Black，以保持从子树的根节点（原先是A，现在是B）的路径的Black节点数保持和原来一样。这里要是Pivot是整棵红黑树的根节点，则需更新Root节点的值。
PtrRBT RBInsert(PtrRBT T, ElementType Val){
PtrRBTNode TempNode = T->Root;
PtrRBTNode NewNode = RBCreateNode(T, Val);

if(NULL == TempNode){
    T->Root = NewNode;
    NewNode->Parent = T->NullNode;
}
else{
    while(T->NullNode != TempNode){
        if(Val < TempNode->Key){
            if(T->NullNode == TempNode->Left){
                TempNode->Left = NewNode;
                NewNode->Parent = TempNode;
                break;
            }
            else{
                TempNode = TempNode->Left;
            }
        }
        else{
            if(T->NullNode == TempNode->Right){
                TempNode->Right = NewNode;
                NewNode->Parent = TempNode;
                break;
            }
            else{
                TempNode = TempNode->Right;
            }
        }
    }
}

T = RBInsertFixUp(T, NewNode);

return T;

}

PtrRBT RBInsertFixUp(PtrRBT T, PtrRBTNode CurrentNode){
PtrRBTNode FNode, GNode, UNode;

while(Red == CurrentNode->Parent->Color){
    FNode = CurrentNode->Parent;
    GNode = FNode->Parent;
    if(GNode->Left == FNode){
        UNode = GNode->Right;
        if(Red == FNode->Color&&Red == UNode->Color){
            FNode->Color = UNode->Color = Black;
            GNode->Color = Red;
            CurrentNode = GNode;
        }
        else{
            if(CurrentNode == FNode->Right){
                T = RBLeftRotate(T, FNode);
                CurrentNode = FNode;
                FNode = CurrentNode->Parent;
            }
            FNode->Color = Black;
            GNode->Color = Red;
            T = RBRightRotate(T, GNode);
        }
    }
    else{
        UNode = GNode->Left;
        if(Red == FNode->Color&&Red == UNode->Color){
            FNode->Color = UNode->Color = Black;
            GNode->Color = Red;
            CurrentNode = GNode;
        }
        else{
            if(CurrentNode == FNode->Left){
                T = RBRightRotate(T, FNode);
                CurrentNode = FNode;
                FNode = CurrentNode->Parent;
            }
            FNode->Color = Black;
            GNode->Color = Red;
            T = RBLeftRotate(T, GNode);
        }
    }
}
T->Root->Color = Black;

return T;

}
查找是一个比较重要且常用的内容，请找一篇哈希表或红黑树实现查找代码。
可以去看STL重map、hash_map容器源码如何实现。也可以看JAVA\Python源码。