hdu1102 hdu1233 hdu4081 hdu4126 最小生成树
Hdu1102 最小生成树 Prime算法(裸):首先有两个集合V{},边的集合E{}。先选择一个点,加入到V集合中,然后选择和
这个V集合中的点相关连的边中最小的,将边的另一头的点加入到V集合中,该边加入到E集合中,V集合中的点是一个连通图,
每次找和这个连通图相连的最短边,来更新。
 View Code
View Code
1 #include <stdio.h>
2 #include <string.h>
3 const int N=105;
4 const int inf=10000000;
5 int map[N][N],n;
6 int vis[N*(N+1)/2];
7 int dis[N*(N+1)/2];
8 void Prime(){
9 int i,j,t;
10 memset(vis,0,sizeof(vis));
11 for(i=1;i<=n;i++){
12 if(i==1) dis[i]=0;
13 else dis[i]=map[1][i];
14 }
15 int loc,sum=0;
16 for(i=1;i<=n;i++){
17 int min=inf;
18 for(j=1;j<=n;j++){
19 if(!vis[j]&&dis[j]<min){
20 min=dis[j];
21 loc=j;
22 }
23 }
24 vis[loc]=1;
25 sum+=min;
26 for(j=1;j<=n;j++){
27 if(!vis[j]&&map[loc][j]<dis[j]){
28 dis[j]=map[loc][j];
29 }
30 }
31 }
32 printf("%d\n",sum);
33 }
34 int main(){
35 int m,a,b;
36 while(scanf("%d",&n)!=EOF){
37 for(int i=1;i<=n;i++){
38 for(int j=1;j<=n;j++){
39 scanf("%d",&map[i][j]);
40 }
41 }
42 scanf("%d",&m);
43 for(int i=0;i<m;i++){
44 scanf("%d%d",&a,&b);
45 map[a][b]=map[b][a]=0;
46 }
47 Prime();
48 }
49 return 0;
50 }
Hdu1233利用Kruskal算法(裸):
Kruskal利用了并查集,将所有的边按照权值从小到大排序,第一条边是必选的,然后看第二条边,如果两个点在一个连通图中,
则该边不选,否则选,如此下去,每次检查一个边要或者不要就取决于两个点是否已经在连通了,连通了则该边不要,不连通则
该边要,并且把该边加到连通图上。
 View Code
View Code
1 #include <stdio.h>
2 #include <iostream>
3 using namespace std;
4 #include <algorithm>
5 const int N=105;
6 int father[N];
7 int find(int x){
8 if(x!=father[x])
9 father[x]=find(father[x]);
10 return father[x];
11 }
12 struct edge{
13 int x,y,v;
14 }e[N*(N-1)/2];
15 int cmp(edge e1,edge e2){
16 return e1.v<e2.v;
17 }
18 int main(){
19 int n;
20 while(scanf("%d",&n)!=EOF&&n){
21 for(int i=0;i<=n;i++){
22 father[i]=i;
23 }
24 n=n*(n-1)/2;
25 for(int i=0;i<n;i++){
26 scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].v);
27 }
28 sort(e,e+n,cmp);
29 int res=0;
30 for(int i=0;i<n;i++){
31 int x=find(e[i].x);
32 int y=find(e[i].y)
33 if(x!=y) {
34 res+=e[i].v;
35 father[x]=y;
36 }
37 }
38 printf("%d\n",res);
39 }
40 return 0;
41 }
HDU4081 最小生成树变形。
题意:
有n坐城市,输入每坐城市的坐标和人口。
现在要在所有城市之间修路,保证每个城市都能相连,并且保证A/B 最大,所有路径的花费和最小
A是某条路i两端城市人口的和
B表示除路i以外所有路的花费的和(路径i的花费为0)
方法:
①先求一棵最小生成树,然后枚举每一条最小生成树上的边,删掉后变成两个生成树,然后找两个集合中点权最大的两个
连接起来。这两个点中必然有权值最大的那个点,所以直接从权值最大的点开始dfs。
为了使A/B的值最大,则A尽可能大,B尽可能小。所以B中的边一定是MST上去掉一条边后的剩余所有边。首先用O(N^2)算出
MST,然后依次枚举,删去MST上的每一条边,MST变成两棵树T1和T2,然后在剩余的边(即不在MST上的边),以及这条删
去的边中找到该边的两点的权值和最大以及能够连接T1和T2的边,A=删去边后的替换边的两点的权值和,B=删去该边后的MST
的值,求A/B最大。则A尽可能大,A分别是T1和T2中最大的两个点,则所有点中权值最大的点一定在A中,由此在MST上从权值
最大的点作为root,开始dfs。递归求出子树中的每个最大的点以及求出A/B的比值,求出最大。
重点在于dfs:
 View Code
View Code
1 int dfs(int u){
2
3 vis[u]=1;
4
5 int temp;
6
7 int t_max=pw[u];//pw是pointWeight每个点的权值
8
9 for(int i=head[u];i!=-1;i=t_e[i].next){//从root开始在MST上dfs
10
11 int v=t_e[i].v;
12
13 if(!vis[v]){
14
15 temp=dfs(v);
16
17 t_max=max(t_max,temp);//每次找出子树中的权值最大点
18
19 ans=max(ans,(temp+maxPoint)/(mst-t_e[i].w));//删除该边
20
21 }
22
23 }
24
25 return t_max;
26
27 }
②求一棵生成树。你可以使其中一条边权值变成0.使得该边两点的权值和除以生成树的边权和最大。
首先求最小生成树,然后枚举每条边。
如果这条边在MST上,那么直接把人口除以(MST - magic road) 即可
但是,如果这条边不在MST上,假设两顶点分别是(u,v)
那么这条边肯定比uàv的MST连边的边的权值都要大。
因为如果要是小的话,那这条边就会加到MST中了。
如果把这条边当作magic road的话,那么这条边以及连接(u,v)的MST的边就组成了一个环了
当前这条边的权值是最大的,要使剩下的路的花费最小,那么肯定要把u v间的最长的一条边给删去就行了
也就是找环中的第二大边了,那么,求任意两点间的最长先预处理的。
求一棵最小生成树,通过类似DP的预处理将每两点之间的最大边求出来,然后,一个二重循环枚举每对点,减掉最大边,
添上点权就行。(解题报告上这么写的,但是个人感觉不需要二重循环,只需要求出权值最大点到其余每个点的路径中最
长的边,然后一重循环,这样又回到了第一种方法上)。
方法①的代码实现(方法②的还没写):
 View Code
View Code
1 #include <stdio.h>
2 #include <math.h>
3 #include <string.h>
4 #include <iostream>
5 #include <algorithm>
6 using namespace std;
7 #define N 1005
8 int edgeNum;
9 double mst,ans;
10 int maxPoint,root;
11 int father[N],pw[N],vis[N];
12 int head[N],t_edgeNum;
13 int find(int x){
14 if(x!=father[x])
15 father[x]=find(father[x]);
16 return father[x];
17 }
18 struct point{
19 int x,y;
20 }p[N];
21 struct edge{
22 int u,v;
23 double w;
24 }e[N*(N-1)/2];
25 struct t_edge{
26 int v,next;
27 double w;
28 }t_e[2*N];
29 void add(int u,int v,double w){
30 t_e[t_edgeNum].v=v;
31 t_e[t_edgeNum].w=w;
32 t_e[t_edgeNum].next=head[u];
33 head[u]=t_edgeNum++;
34 t_e[t_edgeNum].v=u;
35 t_e[t_edgeNum].w=w;
36 t_e[t_edgeNum].next=head[v];
37 head[v]=t_edgeNum++;
38 }
39 void init(){
40 ans=0;
41 edgeNum=0;
42 t_edgeNum=0;
43 mst=maxPoint=0;
44 memset(vis,0,sizeof(vis));
45 memset(head,-1,sizeof(head));
46 for(int i=0;i<N;i++){
47 father[i]=i;
48 }
49 }
50 double getlen(point p1,point p2){
51 return sqrt((double)((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y)));
52 }
53 int cmp(edge e1,edge e2){
54 return e1.w<e2.w;
55 }
56 int dfs(int u){
57 vis[u]=1;
58 int temp;
59 int t_max=pw[u];
60 for(int i=head[u];i!=-1;i=t_e[i].next){
61 int v=t_e[i].v;
62 if(!vis[v]){
63 temp=dfs(v);
64 t_max=max(t_max,temp);
65 ans=max(ans,(temp+maxPoint)/(mst-t_e[i].w));
66 }
67 }
68 return t_max;
69 }
70 int main(){
71 int n,t;
72 scanf("%d",&t);
73 while(t--){
74 init();
75 scanf("%d",&n);
76 for(int i=0;i<n;i++){
77 scanf("%d%d%d",&p[i].x,&p[i].y,&pw[i]);
78 if(pw[i]>maxPoint){
79 maxPoint=pw[i];
80 root=i;
81 }
82 }
83 for(int i=0;i<n;i++)
84 for(int j=i+1;j<n;j++){
85 e[edgeNum].u=i;
86 e[edgeNum].v=j;
87 e[edgeNum].w=getlen(p[i],p[j]);
88 edgeNum++;
89 }
90 sort(e,e+edgeNum,cmp);
91
92 for(int i=0;i<edgeNum;i++){
93 int fa=find(e[i].u);
94 int fb=find(e[i].v);
95 if(fa!=fb){
96 father[fa]=fb;
97 mst+=e[i].w;
98 //printf("(%d,%d) %.4lf\n",e[i].u,e[i].v,e[i].w);
99 add(e[i].u,e[i].v,e[i].w);
100 }
101 }
102 //printf("mst:%.4lf\n",mst);
103 dfs(root);
104 printf("%.2lf\n",ans);
105 }
106 return 0;
107 }
HDU4126最小生成树
题意:
n个点,m个边,然后给出m条边的顶点和权值,其次是q次替换,每次替换一条边,给出每次替换的边的顶点和权值,
求q次替换之后的平均值。其中n<3000,q<10000。
思路:
①首先第一个想到的是暴力,求出Q次MST,显然是不可行的O(q*n^2);
②然后分析一下,利用Prime算法,其中q次替换中不在MST上的边不需要替换,所以时间复杂度降低到O(n^3),但是还是太暴力。
③如果替换的边在MST上,那么将MST上这条边去掉,假设修改的边是(a,b)并把(a,b)的权值修改为c,那个我们把(a,b)边从最小
生成树中去掉,就形成两棵树T1,T2,那么最小生成树就可以由T1,T2加上连接 T1 和T2的权值最小的边。此时这个最小边就是最
有替换边。我想sort一下不在MST上的所有的边,然后找到能连接T1和T2的最小边。TLE了……
④后来看了解题报告,树形dp,从每个点dfs一次,每次把i当成根,其余都是它的孩子,更新dp数组,对于i点为根的除j之外的所有的
子树中的所有点到j距离最小值。每次从一个点pos开始dfs,搜索到最后一个叶子,开始看map[pos][u]的大小,保证(pos,u)
不是MST上的的边,那么一路返回,连接叶子节点的那条边的最佳替换边就是map[pos][u]的大小,再继续返回,
此过程要看,map[pos][...]的大小,其中[...]表示从叶子节点一路返回过来的点。
测试数据:
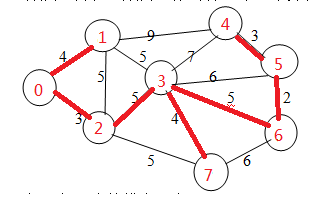
8 14
0 1 4
0 2 3
1 2 5
1 3 5
1 4 9
2 3 5
2 7 5
3 4 7
3 5 6
3 6 5
3 7 4
4 5 3
5 6 2
6 7 6
1
0 1 5
 View Code
View Code
1 #include <vector> 2 #include <stdio.h> 3 #include <iostream> 4 #include <algorithm> 5 using namespace std; 6 const int N=3000+5; 7 const int inf=1000000000; 8 struct edge{ 9 int u,v,w; 10 }e[N*N];//所有的边 11 int n,m,q; 12 int a,b,c; 13 int father[N]; 14 int map[N][N];//map[i][j]表是(i,j)边权值 15 int dp[N][N];//dp[i][j]表示去掉MST上的(i,j)边后的最佳替换边的长度 16 bool vis[N][N];//标记是否在MST上 17 vector<int> Edge[N]; 18 int min(int a,int b){return a<b?a:b;} 19 int find(int x){ 20 if(x!=father[x]) 21 father[x]=find(father[x]); 22 return father[x]; 23 } 24 //用于Kruskal使用 25 int cmp(edge e1,edge e2){ 26 return e1.w<e2.w; 27 } 28 //更新dp[i][j],对于i点为根的除j之外的所有子树中的所有的点到j距离的最小值 29 //确定这些点和j不在一个集合里 30 int dfs(int pos,int u,int fa){//求pos点到以u为根的树及其子树的最小距离 31 int ans=inf; 32 for(int i=0;i<Edge[u].size();i++){ 33 int v=Edge[u][i]; 34 if(v==fa) continue; 35 int tmp=dfs(pos,v,u); 36 ans=min(ans,tmp); 37 dp[u][v]=dp[v][u]=min(dp[u][v],tmp); 38 //通过dfs的返回值来更新dp[i][j] 39 } 40 if(pos!=fa) //保证这条边不是生成树的边,不然不能更新 41 ans=min(ans, map[pos][u]); 42 return ans; 43 } 44 int main(){ 45 while(scanf("%d%d",&n,&m)!=EOF){ 46 if(n==0&&m==0) break; 47 double mst=0,sum=0; 48 for(int i=0;i<n;i++){ 49 Edge[i].clear(); 50 father[i]=i; 51 for(int j=0;j<n;j++) 52 map[i][j]=dp[i][j]=inf, 53 vis[i][j]=1; 54 } 55 for(int i=0;i<m;i++){ 56 scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w); 57 map[e[i].u][e[i].v]=map[e[i].v][e[i].u]=e[i].w; 58 } 59 sort(e,e+m,cmp); 60 for(int i=0;i<m;i++){ 61 a=find(e[i].u); 62 b=find(e[i].v); 63 if(a!=b){ 64 father[a]=b; 65 mst+=e[i].w; 66 Edge[e[i].u].push_back(e[i].v), 67 Edge[e[i].v].push_back(e[i].u); 68 vis[e[i].u][e[i].v]=vis[e[i].v][e[i].u]=0; 69 } 70 } 71 for(int i=0;i<n;i++){ 72 dfs(i,i,-1); 73 } 74 scanf("%d",&q); 75 for(int i=0;i<q;i++){ 76 scanf("%d%d%d",&a,&b,&c); 77 if(vis[a][b]==1) 78 sum+=mst; 79 else 80 sum+=mst*1.0-map[a][b]+min(dp[a][b],c); 81 } 82 printf("%.4lf\n",sum/(double)q); 83 } 84 return 0; 85 }




